Pandemic Mitigation Decision Process

Multi-Discipline Quantitative Analysis

The following article was completed on May 4, 2020. Please read it in the context of that point in time. There was no covid immunization, no mask order, no arrows on floors or plexiglass or any of that stuff.

I neither knew how nor where to publish anything and just sent it via e-mail to a few friends and family. At least, I think I did.

Since I don’t have time to write a new article right now, because the The Real CdC - COVID Facts for Regular People and The CDC Memorandum are taking all my time, and since someone posted something on Twitter X about “ALL” of us were fooled at the beginning, it gave me the idea to post my early articles from 2020. I was naive. But I wasn’t fooled. ;-)

You may find the ideas interesting.

Remember … this was MAY 4, 2020

---

ABSTRACT

This is an article, not a research paper, and will not dive deeply into science and math. It is meant to raise awareness that the current government infrastructure that offers disease mitigation solutions lacks robustness; and that the current solutions are likely causing more harm than good.

We are told by elected leaders that policy decisions are based on science and data. Much of the public does not challenge that premise.

However, “science" and “data" are broad terms and often open to interpretation and opinion.

Data is not a result. Data is only an input to a model that is simulated to produce outputs, or results. The results are interpreted as good or bad, pass or fail, acceptable or unacceptable. It is important to note that simulation results are only as accurate as the model into which you apply the data.

Do not confuse scientists with engineers. Scientists study issues or phenomena. They rarely implement solutions. If a scientist solves an issue, an engineer must then determine if the solution is design-able. Another engineer determines if it is manufacturable (id est, able to manifest in reality). Someone in finance determines if it is potentially unit profitable. A marketing professional performs an analysis to determine if there is a market for the manufactured solution.

Scientists are usually expert in one specific field of study, or one discipline. In the case of Covid-19, scientists crafted solutions and mitigations, then claimed efficacy by stating that their solutions are based on science and data. Their measurement of efficacy relates to models of a singular discipline.

Scientists do not have the multi-discipline knowledge to understand what economists call the “negative externalities” (unintended consequences) of their solutions. Their solutions may solve the issue related to their discipline, yet create three more issues with roots in other disciplines. For example, a plan that minimizes death from a pathogen (microbiological discipline) may cause more deaths from depression (psychological discipline).

To prevent one Covid-19 death is not a net positive outcome if the mitigation activity to save that one life caused one suicide, one domestic violence murder, ten divorces, three heroin overdoses, forty injured in riots, and twenty children to grow up with only one parent, potentially causing lifelong psychoses in a few of those twenty.

This article provides an overview of how to create a team charged with delivering mitigation solutions for epidemics and pandemics. The solutions should be derived from simulations of models from all disciplines and should yield the best overall solution space from which elected leaders can make more informed decisions regarding mitigation policies.

---

INTRODUCTION

In an article, a mechanical engineer explained his fluid dynamics research regarding the oral expression of a virus with and without different types of masks and in situations of coughing, sneezing, singing, exercising, and regular breathing. Like most articles on coronavirus, it was based on research from the singular perspective of one discipline. It did not include the microbiological time decay models of the virus, nor research from any other discipline except fluid dynamics. The decision for or against masks in that article relied solely on the research of the mechanical engineer.

The value delivered to the world by Covid-19 is that it has put on display the lack of multi-discipline modeling and simulation needed to make fully-informed policy decisions. Epidemiologists know epidemiology.

Economists know economics. Psychologists know psychology. Sociologists know sociology. Mechanical engineers know fluid dynamics, thermodynamics, and feedback systems. Microbiologists know decay rates of cells and virus assays under conditions of humidity, temperature, light frequency and intensity ranges, and turbulence.

Unfortunately, there do not appear to be any studies that incorporate multiple disciplines into a model to be simulated and analyzed for minimizing death, minimizing spread, maximizing recovery, or maximizing immunity.

---

ISSUE

The foundational problem to be solved lies in the field of economics, not epidemiology. Do not be confused with the narrow view that economics is a purely financial field of study. To economize a system is to increase the net efficiency of the overall system. This can be achieved through decreasing or increasing inputs or outputs or changing the system to achieve the optimal net result.

In the case of a pandemic, the economist is best equipped to manage all the equations and data from each of the disciplines including epidemiologists, microbiologists, psychologists, sociologists, engineers, physicians, and economists. The economist can create and manage the overall quantitative analysis.

Quantitative analysis (QA) is a mathematical procedure that seeks to minimize or maximize a result (e.g., minimize deaths) based on inputs that are constants (e.g., population size) or variables (e.g., time length of lockdown, wearing of a mask, transportation mode in commute to work). Equations are built from the constants and variables and then used in the QA. A computer program then runs the QA and outputs the solution space.

Currently, the epidemiologists and physicians leading the task force lack the broad understanding to perform multi-discipline analyses. Their mitigation solutions lack sustainability and do not factor in many negative externalities that reside within the purviews of other disciplines.

---

SOLUTION

Create a group (task force, agency, or department) charged with defining a solution space from which policy will be chosen. The solution space will be the result of a multi-discipline quantitative analysis (MDQA). The group should include experts in each of the disciplines necessary to form a robust model.

Automate - The creation of a solution space should be automated in software in order to run billions or trillions of permutations of coefficient variables and sets of input data.

Emulate - The unit models should emulate real world conditions (id est, those possible in reality).

Generate - Each discipline will generate its unit (one discipline) simulation models.

Integrate - All the unit models will be integrated into one large, robust MDQA model.

Simulate - Run the MDQA to produce the solution space from which policy should be derived.

---

High-Level EXAMPLE

Population can be elaborated into age and gender strata, co-morbidities by type, general location (urban, suburban, rural), personal or public transportation preferred, or dine-out, take-out, or home-prepared meals preferred. However, for simplicity in this example, total population will simply be one variable N.

Equations will be represented as functions in this example because the equations are non-linear and can contain double and triple integral calculus. Again, this is only an article, not a research paper.

The MDQA team should approach this as an engineering exercise and not an academic exercise. They need to produce something that is practical for the real world. The MDQA team should always keep in mind that pragmatism must reign over complexity. Keep the equations simple whenever possible.

In this example, the objective is to minimize death overall.

SIR Model - The Epidemiological Viewpoint (If you don’t like math, skip to the Multi- Discipline Model discussion)

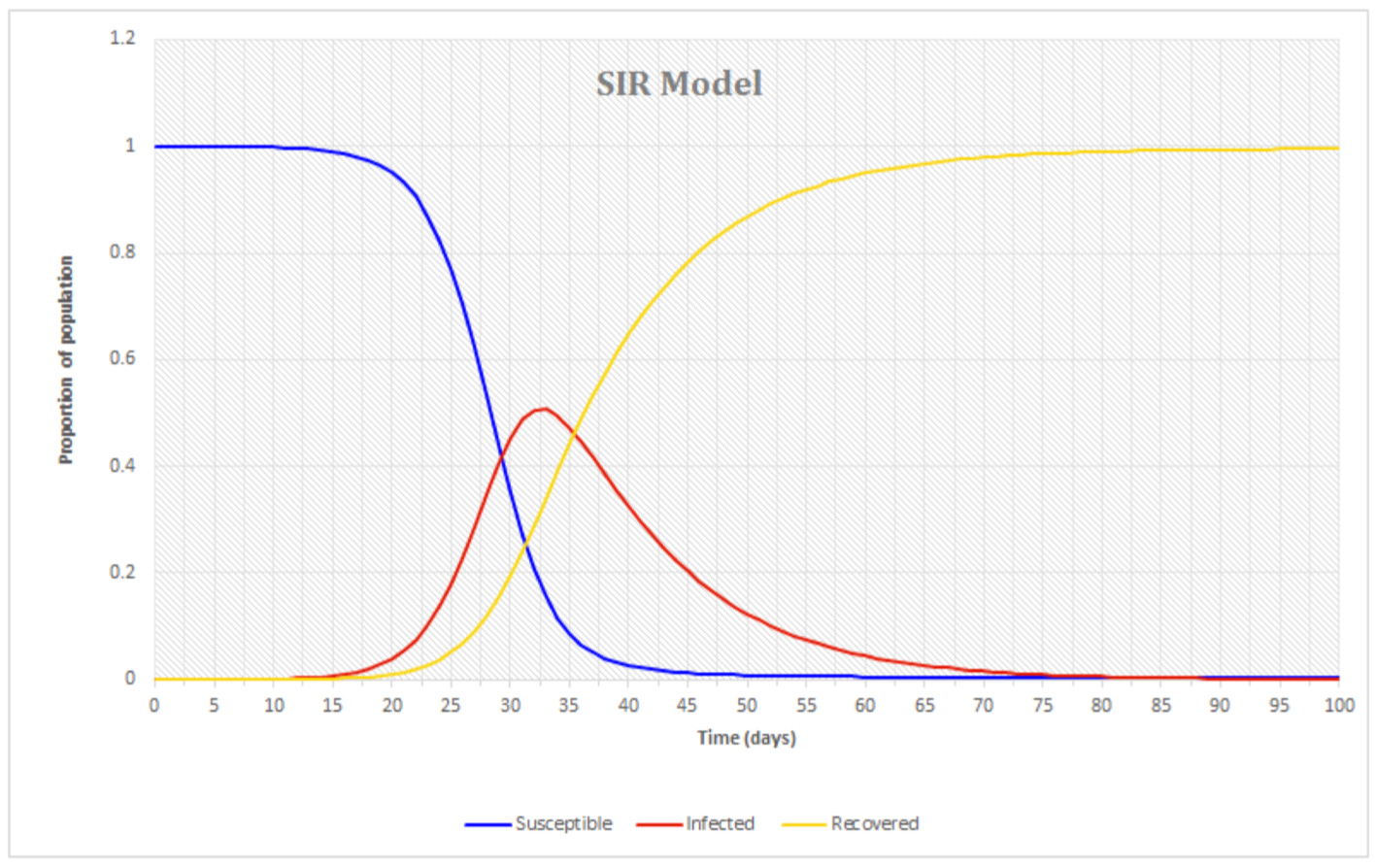
In the SIR Model, the total Population (N) is comprised of three groups: Susceptible (S), Infectious (I), and Recovered (R). People progress from Group S to Group I to Group R.

N = S + I + R

S, I, and R are functions of time (t). At t = 0, S(0) = N, while I(0) and R(0) both are zero. At time t = 1, I(1) becomes 1 or more, while S(1) = N - I(1). If the recovery period is 14 days, then at t = 15, the number infected at t = 1, move from I to R.

Thus, R(15) = I(1). For any given point in time, the original equation for total population holds true.

N = S(t) + I(t) + R(t)

Rather than observing the complex functions themselves, see the graph to understand how the three functions are related in time. S(t) begins at total population, while I(t) and R(t) begin at 0. As people become infected, I(t) rises and S(t) falls, while the two added together equals N. As people recover, R(t) rises. Notice that S(t) can only diminish in time, R(t) can only rise in time, and I(t) rises exponentially, levels off, and then falls eventually to zero. (Smith, retrieved 2020)

In the graph, the variables used are proportions of population N. The functions graphed are:
blue s(t) = S(t) / N
red i(t) = I(t) / N

yellow r(t) = R(t) / N

Thus, the total population would be represented as “1” on the vertical axis of the graph. Notice at t ~32 days, s(~32) and r(~32) are ~ 0.25 each, while i(~32) is ~ 0.5. The total ~= 1.00.

For purposes of this article, and diverging from classical epidemiological constructs, the death rate will be those who perish as a percentage of those who are infected, denoted D(t); and in population proportion form, it will be d(t). Assume that d(t) is simply a portion of i(t - 14), if it takes 14 days from infection to death. As an example, if there is a 1% chance of dying after being infected, then d(t) = 0.01i(t - 14). Now imagine d(t) on the graph. It will be a curve shaped similarly to i(t), but far below it and shifted right 14 days. When N is large, NUSA > 327 million people, D becomes significant. 1.0% of 327 million is 3.27 million people.

Envision that the graph will flatten and lengthen or become more compressed and steep depending on the spread rate (the famous R0), recovery time, and other factors.

In the next discussion, note the i(t) red curve and how it almost resembles a bell curve. The smaller portions on the left and right are called the left and right tails.

It is important to understand that the calculation of total deaths is the area under curve D(t). For any point in time x, total deaths can be represented as:

𝜮 D(t), where t = 0 to x

Multi-Discipline Model

(No math. Just commentaries on models)

Vaccine Commentary

In ideal circumstances, a vaccine would become available at a point in time and no one would die after that point in time. Thus, if the vaccine occurs late, then it will be a vertical line intersecting the graph of the death rate in the right tail area of the curve. The area under the curve to the right of the vertical line would be the lives saved by the vaccine. The farther to the right, the fewer lives are saved. Thus, the MDQA would include equations of vaccine introduction at points in time. Under non-ideal, real world conditions, the vaccine function would factor in the proportions of people who would receive and refuse the vaccine. Psychology and sociology are pertinent to this part of the discussion. There are those who believe vaccines should be forced on people by the government for the greater good of society. This must also be modeled.

Mitigation Measures

Lockdown or shelter-in-place orders are likely to have a significant effect on the curves. But in what way? Will they stop the spread or stop people from dying? In the case of Covid-19, these stringent orders do not stop the spread or deaths. They merely flatten the curve, which lengthens it in time. Bear in mind that the area under the curve does not change when the curve is flattened unless there are other factors considered. If a vaccine would be available soon, then flattening the curve would be a significant saving of life as the vertical line would push into the heart of the bell-shaped D(t) curve. This is not the case with Covid-19. And time will be far into the right tail with or without these drastic mitigation measures. Thus, the area under the SIR model death curve will be nearly the same in the end with or without mitigation measures.

It is vitally important that mitigation measures be modeled in the MDQA. Without modeling mitigation factors and externalities, we are blind to potential future results.

Other Disciplines

How will the mitigation measures affect the overall death rate?

As equations are added for other disciplines, the area under the curve only grows. These are externalities, or issues external to epidemiology.

Psychologists will add equations to project the suicide rate as a function of time for each type of mitigation measure. They’ll do the same for domestic violence homicides, overdose deaths, and other factors.

Mechanical engineers and microbiologists will add equations that relate to mitigation measures such as mask wearing at home, in office buildings, or outdoors. UV light from the sun causes a significantly faster decay rate of the virus assays as they float in air or on surfaces. Temperature, humidity, air turbulence (outdoors or from HVAC systems indoors) are all factors that must be modeled and input into the MDQA model.

As the mitigation models from multiple disciplines are added to the overall MDQA, they change the area of death minimization among all the equations.

Though one would expect that mitigation should diminish the area under the curve, it is obvious that mitigation measures raise the overall death rate. This compels the formation of an MDQA team to study all aspects of the virus, while including studies of mitigation measures and the externalities from them.

---

CONCLUSION

Measures are being taken to mitigate the spread of the virus. These measures have been recommended from one single discipline. They do not factor in other disciplines. The mitigation measures being applied may very well grow the total death figure rather than diminish it. Wearing masks outdoors may very well have no effect at all; or the masks may cause higher risk of infection because you now have a highly concentrated virus assay source that, if jostled, may shed an enormous amount of virus all at once. People frequently touch their faces. They touch their faces more when wearing masks. When touching their mask, they touch a much higher concentration of virus assays than when they touch their face without a mask.

While drastic mitigation measures flatten the curve, they do nothing to reduce the overall death total in the long run; and such measures only serve to increase total death from externalities.

It is obvious to any thinking person that the government, especially the CDC and NIH, has not considered important factors and does not know much about the resulting externalities. Given the premise that they are blind to externalities because they have not studied them, how can they expect anyone to believe that these measures are necessary or even helpful? For those who think for themselves, it is conceivable and even likely that the measures cause more harm than good.

The public should demand that MDQA be used and that the MDQA methods and results be made public. There is no reason for the CDC to hide methods, equations, and data. Demand transparency. Demand better science and data.

---

REFERENCES

• (graph taken from) Collins, J., Abdelal, N. Spread of Disease. no date or publication listed. Retrieved 2020-05-08 from https:// calculate.org.au/wp-content/uploads/sites/ 15/2018/10/spread-of-disease.pdf

• Smith, D., Moore, L. The SIR Model for Spread of Disease - The Differential Equation Model. Mathematical Association of America. Retrieved 2020-05-08 from https://www.maa.org/press/ periodicals/loci/joma/the-sir-model-for-spread-of- disease-the-differential-equation-model